Conor Deegan | Diffie–Hellman key exchange

Diffie–Hellman key exchange

Introduction

Diffie–Hellman key exchange establishes a shared secret between two parties that can be used for secret communication for exchanging data over a public network. An issue with symmetric cryptography is that it requires a secret to be communicated through some sort of trusted intermediary in order for both parties to have access to the same key. This is not only inefficient but, more importantly, at risk of messages being intercepted and decrypted by a third party who acquired the key during the initial key exchange. The Diffie Hellman algorithm allows for negotiating a symmetric key without the need for this trusted intermediary.

Ultimately the Diffie-Hellman key exchange algorithm exploits the fact that discrete exponentiation can be computed efficiently, whereas discrete logarithms cannot.

How it works

The Diffie-Hellman algorithm is as follows:

Two numbers $p$ and $g$ are chosen such that $p$ is a large prime and $g$ is a primitive root of $p$ . This is explained further below. Both of these numbers can be made public.
Alice chooses a random number $a$ such that $1 \le a \le p-2$ . This becomes Alice’s private key.
Alice computes $A = g^{a} \mod p$ . This becomes Alice’s public key.
Bob chooses a random number $b$ such that $1 \le b \le p-2$ . This becomes Bob’s private key.
Bob computes $B = g^{b} \mod p$ . This becomes Bob’s public key.
Alice and Bob can now exchange $A$ and $B$ in public.
Alice computes $K_a$ as $K_a = B^{a} \mod p$ .
Bob computes $K_b$ as $K_b = A^{b} \mod p$ .
Alice and Bob now have a shared secret as $K_a = K_b$

Proof:

$K_a = B^{a} \mod p = (g^{b})^{a} \mod p = g^{ab} \mod p$

$K_b = A^{b} \mod p = (g^{a})^{b} \mod p = g^{ab} \mod p$

Alice and Bob can now perform symmetric encryption and decryption given they possess the same key.

We will now look at each of these steps in more detail.

Step 1 - Generating a large prime

This first step is to generate a sufficiently large prime, $p$ where $p$ is typically a 2,048-bit or 4,094-bit number.

A common way to generate a large prime $p$ is as follows:

Create $\sigma$ , a random $n$ -bit number (e.g 2,048-bits). It should be the case that $\sigma$ is odd as no prime number, with the exception of 2, is even. Thus we select a decimal number in the range $2^{n-1} + 1$ up to $2^n -1$ . We call $\sigma$ the prime candidate.
We can then perform a low-level primality test by checking if $\sigma$ is divisible by any of the first $k$ prime numbers (this list of primes is precomputed). The value of $k$ should be as large as possible. If $\sigma$ is divisible by any of these pre-computed primes, the prime candidate is composite and we return to step 1.
Once we find a $\sigma$ that passes this low-level primality test, we can perform a high-level primality test known as the Miller–Rabin primality test. In the case of testing for primality of extremely large numbers, such as those used in Diffie-Hellman, a deterministic method is not feasible in terms of compute power. Instead, the Miller–Rabin primality test uses a probabilistic approach. It tests a prime candidate ( $\sigma$ ) for primality many times. Each time the test passes the candidate has a 75% chance of being prime. By performing many iterations, we can increase the probability that such a candidate is in fact prime. Enough tests should be performed such that the probability of the prime candidate being composite is less than $\frac{1}{2^{128}}$ . If any of the iterations fail, we return to step 1.

With the above algorithm we can now generate $p$ , a 2,048-bit prime.

Primitive roots

In order to compute $g$ , we must first briefly look at groups, subgroups, and primitive roots.

A group is a set of numbers, together with an operation (addition/multiplication), which is closed within the set. What this means is that any operation performed on an element in a group will result in another element within that group. We denote a group as $\mathbb{Z}^{*}_p = {1,…,p-1}$ - this denotes a group with multiplication $\pmod{p}$ .
A subgroup, is a subset of a group which forms a group by itself.
A primitive root of a group $p$ is an integer $g$ such that every integer relatively prime to $p$ is congruent to a power of $g \pmod{p}$ .

Definition of congruent: For a positive integer $n$ , the integers $x$ and $y$ are congruent mod n, if their remainder when divided by $n$ are the same. For example: $24 \mod 7 = 3$ and $31 \mod 7 = 3$ . Therefore, we can say that $24$ and $31$ are congruent mod 7. We write this as $24 \equiv 31 \pmod{7}$ .

With this we can now define $g$ : $g$ is a primitive root modulo $p$ , if for every integer relatively prime to $p$ , there is an integer $z$ such that $a \equiv g^z \mod p$ where $a$ is the integer relatively prime to $p$ .

Okay so that’s all a bit abstract, we will now look at an example.

Example: is $2$ a primitive root modulo $5$ ? Here, $g=2$ and $p=5$ . The integers relatively prime to 5 are 1,2,3,4.

For $a = 1$ :

$2^0\mod 5 = 1\mod 5 = 1 = a$

For $a = 2$ :

$2^1\mod 5 = 2\mod 5 = 2 = a$

For $a = 3$ :

$2^3\mod 5 = 8\mod 5 = 3 = a$

For $a = 4$ :

$2^2\mod 5 = 4\mod 5 = 4 = a$

Thus, for every integer relatively prime to $p=5$ , there is an integer $z$ such that $a \equiv 2^z \mod n$ . Therefore, $g=2$ is a primitive root modulo $5$ .

As part of the Python implementation, you can see a program that finds the primitive root $g$ of $p$ here.

Selecting a private key

Now that we have prime $p$ and a primitive root $g$ , we can move on to selecting a private key. To select a private key, Alice simply selects a random number $a$ such that $1 \le a \le p-2$ . The reason for the bounds are as follows: if you select a = 0, then $g^{a} = 1$ which is insecure. If $a$ is chosen as $p-1$ , given Fermants little theorem you get $a^{p-1} \equiv 1 \mod p$ which is insecure. Finally it is pointless to select $a$ such that $a > p$ as it will be reduced with $mod(p)$ .

Computing a public key

To compute the public key $A$ , Alice can compute the following $A = g^{a} \mod p$ . This is the one-way function used in Diffie-Hellman. Given $A$ , it is computationally hard to compute $a$ , however if you are give $a$ is it relatively straightforward to compute $A$ . Hence why it is safe to share your public key, well, publicly. This will be discussed in more detail in the security section below.

Generating the shared secret

We have already seen this proof:

$K_a = B^{a} \mod p = (g^{b})^{a} \mod p = g^{ab} \mod p$

$K_b = A^{b} \mod p = (g^{a})^{b} \mod p = g^{ab} \mod p$

This shows that once Alice and Bob share their respective public keys, it is trivial for them to compute a shared secret. However, without knowledge of one of the private keys it is computationally very difficult to compute this shared secret. See security section below.

Security of Diffie-Hellman

How large does the prime $p$ have to be:

Simply put, as large as possible. Although in practice there are limits as to how large $p$ can be (computation effort, etc).

Typically $p$ is chosen as either a 1,024-bit prime or a 2,048-bit prime. The Snowden documents suggest that the NSA is now capable of breaking 1,024-bit Diffie-Hellman is some cases. Sticking with 2,048-bit primes is common.

What happens if $g$ is not a primitive root:

If $g$ is not a primitive root of $p$ , $g$ may generate a smaller subgroup within $p$ . This means that the overall security of the system is now proportional to the order of $g$ rather than the order of $p$ . This means that rather than the number of operations to brute force a private key being $p-1$ , an attacker could perform a brute force attack proportional to the order of $g$ instead.

Discrete logarithm problem:

Given a public key $A$ , no efficient method is known to compute $a$ such that $A = g^a \mod p$ . This is known as the discrete logarithm problem. This is why sharing your public key is safe.

One option for an attacker, Mallet, would be to perform a brute force attack. I.e compute $A$ for all $a$ = 1, 2, 3,…, p-2. This gives a complexity of $O(p)$ and a very large prime (2,048-bits) makes this infeasible. However, given $a$ it is trivial to compute $A$ using exponentiation by squaring.

Some algorithms exist that perform better than a rudimentary brute force attack, see the index calculus algorithm. The record discrete logarithm computation is for a 795-bit number, see here, this is considerably lower than the 2,048-bit numbers commonly used.

Non-Authenticated key-agreement protocol

Diffie-Hellman is a non-authenticated key-agreement protocol, meaning it does not provide any authentication of the parties involved. This leaves it vulnerable to man-in-the-middle attacks.

However, the Diffie-Hellman key-agreement protocol forms the basis for a variety of authenticated protocols. One common way to mitigate against a man-in-the-middle attack is to use a public private key pair where parties, or trusted third parties, can sign their Diffie-Hellman public keys to prove ownership.

Man in the Middle Attack

As mentioned, Diffie-Hellman is susceptible to man-in-the-middle-attacks as there is no mutual authentication of the parties involved.

This attack is relatively straightforward:

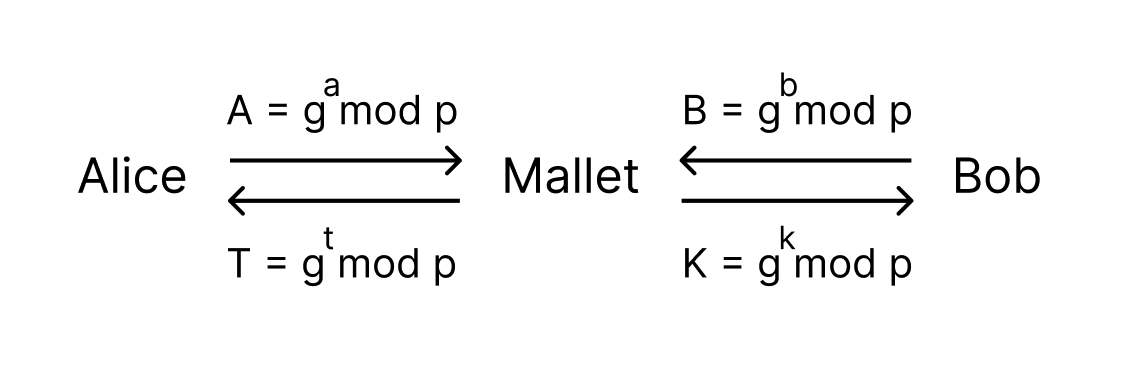Man-In-The-Middle A Man in the Middle Attack

Mallet sits in between Alice and Bobs communication. He is then able to create a shared secret with Alice and a different shared secret with Bob. Neither Alice nor Bob are aware that they are not dealing directly with the other party. Once Mallet has the two shared secrets he can simply decrypt incoming messages from Alice using his shared secret with Alice, read them, encrypt them with his shared secret with Bob and forward them on. Mallet can now also alter the message sent.

A working example is demonstrated in python here.

Implementation in Python

A complete implementation of Diffie-Hellman, along with a sample Man in the Middle attack, in Python can be found here. The code should be self explanatory given the information above.

References

Note: these references exclude hyperlinks included throughout the document.

Disclaimer: Do not use this to secure any information. This code is purely to be used for educational purposes only.

← Back